


Next: About this document ...
Observationelle Værktøjer
Magnitudes and their measurements
Measuring a magnitude means measuring the amount of light from an object
on the sky with a given instrument at a given time. The instrument and
observing conditions defines a response function, which takes into account
the transmission of the optics, the filter selected and the quantum
efficiency of the detector, which we can include in one function
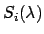 .
The index i is indication of the choice of filter (i = V is one choice)
If the flux at the distance of the earth from the object is
.
The index i is indication of the choice of filter (i = V is one choice)
If the flux at the distance of the earth from the object is
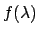 ,
we will get a measurement, recorded as nph detected photons directly by a
photoelectric photometer (or similar if integrated over an area of a CCD image),
where
,
we will get a measurement, recorded as nph detected photons directly by a
photoelectric photometer (or similar if integrated over an area of a CCD image),
where
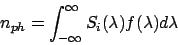 |
(1) |
For historical reasons we now define the imagnitude by
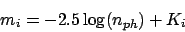 |
(2) |
where the constant Ki depends on
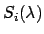 .
Magnitudes are used to compare the brightness of stars in different
spectral regions and mostly occurs as differences:
.
Magnitudes are used to compare the brightness of stars in different
spectral regions and mostly occurs as differences:
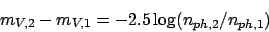 |
(3) |
where the magnitude difference is related to the ratio of photon
counts. As we are using the same filter system V, the constant
disappears.
Extinction
The atmosphere causes absorption of the light and reduces the flux from
the star. The flux received at the telescope is related to the flux
above the atmosphere by the relation
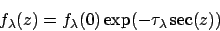 |
(4) |
where z is the zenith distance and
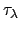 is the
optical depth of the atmosphere. Converting to magnitudes this gives
a relation between the magnitude measured at the ground and above the
atmosphere
is the
optical depth of the atmosphere. Converting to magnitudes this gives
a relation between the magnitude measured at the ground and above the
atmosphere
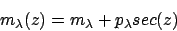 |
(5) |
where
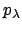 is called the extinction coefficient.
By measuring a star at different zenith distances z and plotting
is called the extinction coefficient.
By measuring a star at different zenith distances z and plotting
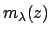 versus
versus 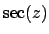 ,
one can derive the extinction
coefficient
,
one can derive the extinction
coefficient
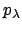 .
This requires a stable photometric
night. Cirrus clouds will spoil the measurements. Once the extinction
is removed, we can discuss magnitudes as they would have been measured
outside the Earth's atmosphere.
.
This requires a stable photometric
night. Cirrus clouds will spoil the measurements. Once the extinction
is removed, we can discuss magnitudes as they would have been measured
outside the Earth's atmosphere.
Colours
If we use different filters it is possible to define a colour by
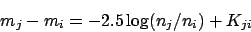 |
(6) |
where we again have an arbitrary constant Kji. Examples of colours
are mB-mV or just B-V.
In order to compare magnitudes and colours measured at different
telescopes with different filteres and detectors, a system of
standard stars are setup, which defines the standard system.
If you measure magnitudes and colours for these stars you will
get magnitudes and colours, which we will call system
measurements. For the standard stars you want to transform
your measurements to the standard system, which you can
by measuring enough standard stars to enable you to determine
the coefficients of linear transformations (for the B and V magnitudes)
|
Bi,std = a0 + a1Bi,instr + a2(Bi,instr - Vi,instr)
|
(7) |
and
|
Vi,std = b0 + b1Vi,instr + b2(Bi,instr - Vi,instr)
|
(8) |
By observing enough standard stars covering a range in magnitudes
and colours, the six coefficients can be determined from a least
square solution to the set of equations for all standard stars.
The magnitudes should be corrected for extinction, before solving
for the transformation. Once the transformation is known, it can
be used for all stars measured.
Sometimes it can be difficult to observe standard stars, because
they are too bright for a large telescope, but the grid of stars
defined as standards is expanding.
The distance
The magnitudes defined above is the apparent magnitudes as
measured from our position in the Universe. To compare stars at different
distances the absolute magnitude is defined, written with a
capital M, which is the magnitude one would observe, if the object was
10 parsecs away. If we also include the effect of interstellar
absorption due to dust and gas in the Galaxy, we get the relation
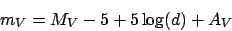 |
(9) |
where d is the distance in parsecs and AV the absorption in the
V system. This latter absorption is related to the colour excess
|
E(B-V) = (B-V)obs - (B-V)0
|
(10) |
which can be measured by the effect observed in Colour-Magnitude
diagrams for open clusters. It can also be determined from multicolour
measurements.
The relation between absoprtion and colour excess is sort of universal
due to the similarity of dust clouds. Thus one can use a relation
to fix the interstellar absorption once the reddening E(B-V) is
measured.
Absolute magnitudes of stars can be directly comapred, as the
distance has now been eliminated. Still the measurement depends on
the filter system. In order to compare the energy output in terms
of the total luminosity of the star L, one must be able to calculate
or measure the Bolometric Correction, which relates the absolute
bolometric magnitude to the V magnitude
Once the B.C. is known for a given star, and it depends on spectral type and
gravity of the star, one can compare the luminosities of stars.
Often one will use the Sun as the reference and express the luminosity in
solar units
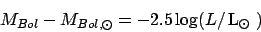 |
(13) |
where the absolute bolometric magnitude for the Sun is wellknown.
Remember that the luminosity is related to the effective temparature Teffand the stellar radius by
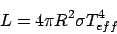 |
(14) |
As you will realize, the transformation of observed magnitudes into the
basic properties of stars in terms of L, R and Teff is not
straightforward and depends on a number of uncertain calibrations.



Next: About this document ...
Soeren Frandsen
2007-02-13
![]() .
The index i is indication of the choice of filter (i = V is one choice)
If the flux at the distance of the earth from the object is
.
The index i is indication of the choice of filter (i = V is one choice)
If the flux at the distance of the earth from the object is
![]() ,
we will get a measurement, recorded as nph detected photons directly by a
photoelectric photometer (or similar if integrated over an area of a CCD image),
where
,
we will get a measurement, recorded as nph detected photons directly by a
photoelectric photometer (or similar if integrated over an area of a CCD image),
where