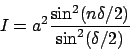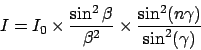Next: About this document ...
Observationelle Værktøjer
The equations of spectroscopy
The prism
The angles involved for rays passing a prism are connected through
Snell's law, which for the angles with the normal to the surfaces
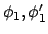 and
and
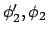 states
states
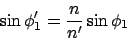 |
(1) |
and
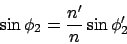 |
(2) |
where
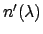 is the refractive index for the glass and
is the refractive index for the glass and 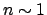 is the refractive index of air. The two angles inside the prism are
connected through the prism top angle
is the refractive index of air. The two angles inside the prism are
connected through the prism top angle 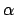
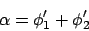 |
(3) |
The change of the direction of the ray exiting the prism with respect
to the incoming ray is given by
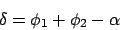 |
(4) |
The minimum deviation 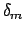 is found when the angles
is found when the angles
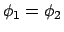 in which case
in which case
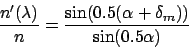 |
(5) |
By measuring 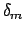 one can determine
one can determine
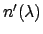 .
With a table
of
.
With a table
of
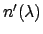 ,
the angular dispersion
,
the angular dispersion
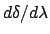 can be
found. In the notes we have a case, where we find the dispersion
to be 0.6 deg/Å. With a focal length of the camera of
fcam = 500 mm
the linear dispersion becomes
can be
found. In the notes we have a case, where we find the dispersion
to be 0.6 deg/Å. With a focal length of the camera of
fcam = 500 mm
the linear dispersion becomes
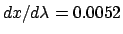 mm/Å.
mm/Å.
The grating
The light transmitted from one slit will be diffracted according to
the wellknown formula
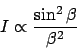 |
(6) |
where
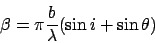 |
(7) |
The phase shift one ray relative to the other is given by AB+BC, which
comes to a phase shift 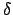
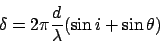 |
(8) |
The electrical field from all slits is now made up of sums over terms
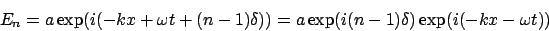 |
(9) |
Summing all terms from the n slits give a total amplitude of
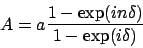 |
(10) |
The intensity I measured is the square of the electrical field or
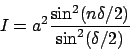 |
(11) |
Combining the results from the diffraction of one slit with the sum
over the total set of slits one gets
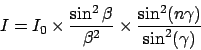 |
(12) |
and 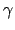 is defined by
is defined by
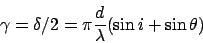 |
(13) |
The last factor will give maximum contribution when the En contributions
are in phase, which happens for integers m satisfying
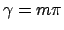 .
This leads to the very basic equation (the grating equation)
.
This leads to the very basic equation (the grating equation)
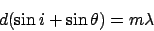 |
(14) |
Now, several things can be derived. The theoretical resolution can be
derived, which defines the smallest wavelength difference that can be
measured. The argument is to move so far from a given wavelength 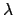 ,
where
you have constructive interference to a wavelength
,
where
you have constructive interference to a wavelength
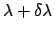 ,
where you have destructive interference. This gives the answer
,
where you have destructive interference. This gives the answer
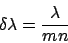 |
(15) |
One defines the theoretical resolution R of a grating by the ratio
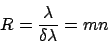 |
(16) |
The angular dispersion is found by differentiation of the grating equation
and gives
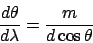 |
(17) |
To get a high dispersion, it obviously pays off to work with a grating
that can be used in a high order mode m.
Finally one can find the distance between subsequent orders m and m+1as
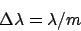 |
(18) |



Next: About this document ...
Soeren Frandsen
2007-02-28
![]() and
and
![]() states
states